Cheap Talk
To give a formal definition, cheap talk is communication that is:
- costless to transmit and receive
- non-binding (i.e. does not limit strategic choices by either party)
- unverifiable (i.e. cannot be verified by a third party like a court)
这个是wiki里的，在这篇文章里的定义：Farrell, Joseph (1987). “Cheap Talk, Coordination, and Entry”. The RAND Journal of Economics. 18 (1): 34–39. JSTOR 2555533.
剩下的是这篇文章中的我的笔记
- Crawford, Vincent P., and Joel Sobel. “Strategic information transmission.” Econometrica: Journal of the Econometric Society (1982): 1431-1451.
- Notes: https://econweb.ucsd.edu/~jsobel/Paris_Lectures/20070612_cheaptalknotes.pdf
这篇文章是经典中的经典，cheap talk和bayesian persuasion都拿了诺贝尔经济学奖，bp中的通信阶段就是cheap talk，作者也claim说了persuasion就是sender’s commitent + cheap talk
里面的这个二次例子也非常重要，在很多文献中都出现了，性质很好，而且解释得很明白，结果要算的话也很简单（但我没有check过是否这个是在这里第一次提出的）
之前只是看了setting，没有仔细去看里面的分析，现在补上
The Model
- Sender $S$ and receiver $R$
- Sender has private information. It observes a random variable $m$. Density is $f(m)$, supported on $[0,1]$
- “Supported” means greater than zero.
- $S$ has a twice continuously differentiable von Neumann-Morgenstern utility function $U^S(y,m,b)$
- $y$ is a real number and is the action taken by $R$ upon receiving $S$’s signal $n$
- $b$ is a scalar parameter and is used to measure how nearly agents’ interests coincide.
- $R$’s twice continuously differentiable von Neumann-Morgenstern utility function is denoted $U^R(y,m)$
- All aspects of the game except $m$ are common knowledge. 包括了双方的收益函数
Assumptions of utility functions: for each state $m$ and for $i=S,R$
- $U_1^i(y,m)=0$ for some $y$
- $U_{11}^i(\cdot)<0$
- $U_{12}^i(\cdot)>0$
Remarks:
- $U_{1}$这个符号表示的是U对第一个变量求偏导，就是对y求导
- 这个也叫边际效用，一般情况下自变量是代表商品数量
- $U_{12}$这个符号表示的是U对第一个变量求偏导完接着对第二个变量求偏导
- 假设1和2是为了让$U^i$ has a unique maximum in $y$ for each given $(m, b)$ pair
- 假设3是叫sorting condition，很多signaling literature里都有的假设
- 假设3代表了state $m$和边际效用是正相关的，并且和$y$的最大值是成正相关的
- 求解最优的$y$需要它的偏导等于0：$U_{1}^i(y,m)=0$，这里的$y$和$m$用隐函数定理求梯度，implicit function theorem
- $\frac{dy}{dm} = -\frac{U^i_{12}}{U^i_{11}}$
- 我们假设了$U^i_{11}<0$，上面的假设2，所以这里的$\frac{dy}{dm}$大于0
- 就是说，在$U_{1}^i(y,m)=0$的情况下，$\frac{dy}{dm}>0$，所以$m$越大则满足偏导为0的$y$越大（最优$y$越大）
假设 \(F(x, y) = 0\)，其中 \(F: \mathbb{R}^{n+m} \to \mathbb{R}^m\)，且 \(y \in \mathbb{R}^m\) 是 \(x \in \mathbb{R}^n\) 的隐函数 \(y = g(x)\)。如果隐函数 \(g(x)\) 存在并可微，则 \(g(x)\) 的导数可以通过以下公式表示：\(\frac{\mathrm{d} g}{\mathrm{d} x} = -\left( \frac{\partial F}{\partial y} \right)^{-1} \frac{\partial F}{\partial x}.\)
Procedure:
- $S$ observes its type $m$ (or environmental state)
- $S$ sends a signal $n$ to $R$ (the signal may be random, and can be viewd as a noisy estimate of $m$)
- $R$ processes the information in $S$’s signal (update its posterior belief about $m$ using Bayes rule)
- $R$ chooses its action to optimize its posterior expected reward
Remarks:
- 因为$S$能观测一个私有信息，然后$R$其实希望知道这个信息（因为这和他的收益相关），那么用mechanism design的术语来看的话，其实这里$S$是agent，而$R$是principal，这和我之前的理解不太一样
- 这个过程就是Bayesian persuasion里的通信的过程，其实应该先接触这个再学BP，我是反过来了
Equilibrium
Bayesian Nash Equilibrium
An equilibrium consists of a family of signaling rules for $S$, denoted as $q(n\mid m)$, and an action rule for $R$, denoted $y(n)$, such that:
- for each \(m \in[0,1], \int_N q(n \mid m) d n=1\), where the Borel set \(N\) is the set of feasible signals, and if \(n^*\) is in the support of \(q(\cdot \mid m)\), then \(n^*\) solves \(\max _{n \in N} U^S(y(n), m, b)\); and
- for each \(n, y(n)\) solves \(\max _y \int_0^1 U^R(y, m) p(m \mid n) d m\), where \(p(m \mid n) \equiv q(n \mid m) f(m) / \int_0^1 q(n \mid t) f(t) d t .\)
Remarks:
- 第二个条件中，where后面是贝叶斯，意思是receiver选的动作会优化它自己的后验收益期望
- 所以这里看起来不是用后验来用bayes decision rule先猜一个最可能的state，而是拿整个后验分布来优化收益期望
- 第一个条件中，前两个小条件是用来约束$q$是一个概率，最后那个条件很绕，意思是假如receiver的策略$y(n)$是给出的，那么它发信号会引起一个确定的动作$y$，那么有一个信号$n$是可以最大化sender自己的收益的，这个$n$记为\(n^*\)，那么sender的signaling scheme的约束就是\(n^*\)的概率大于0就行了
- 大于0就行，还是比较宽松的
- 但它不能一直发这个信号，因为要引入noise来干扰receiver的后验从而印象它的决策
- 再看第二个条件，现在我们想结合之前的假设看看有什么性质
- 发现receiver的优化目标对$y$是strictly concave的
- 因为$U^R_{11}<0$
- 求两次梯度也没事，后面那个$p$里没$y$，所以只是系数，求完之后还是大于0
- 所以均衡中，$R$不需要mixed strategies
- 发现receiver的优化目标对$y$是strictly concave的
Partition Equilibrium
When agents’ interests differ, all equilibria in this model are partition equilibria of a particular kind.
Let $a(N) \equiv\left(a_0(N), \ldots, a_N(N)\right)$ denote a partition of $[0,1]$ with $N$ steps and dividing points between steps $a_0(N), \ldots$, $a_N(N)$, where $0=a_0(N)<a_1(N)<\cdots<a_N(N)=1$.
Define, for all $\underline{a}, \bar{a} \in[0,1], \underline{a} \leq \bar{a}$,
\[\bar{y}(\underline{a}, \bar{a}) \equiv\left\{\begin{array}{lll}\arg \max \int_{\underline{a}}^{\bar{a}} U^R(y, m) f(m) d m & \text { if } \underline{a}<\bar{a}, \\ y^R(\underline{a}) & \text { if } \underline{a}=\bar{a} .\end{array}\right.\]Remarks:
- Partition equilibrium是之前的文章提出来的
- 第一句话是要证的，是Theorem 1的内容；我没去看
- 这个$a$就是个实数，看他写在$y$的变量里面所以是当成信号的分割
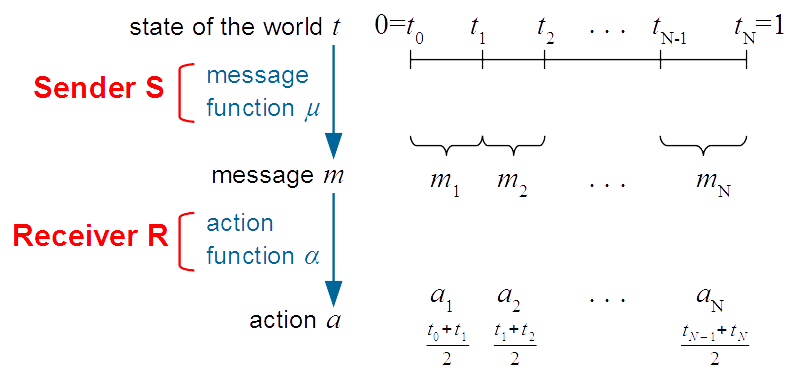
- 这个配一张wiki的图就能懂了，图里的$t, m, a$分别对应我们这里的$m, n, y$，上面的定义说的是receiver的行为，但是这里的$y$和上面的不同，这里的期望是先验的
https://upload.wikimedia.org/wikipedia/commons/6/6a/Cheap_talk.png
Theorem 1:
Suppose $b$ is such that $y^S(m, b) \neq y^R(m)$ for all $m$. Then there exists a positive integer $N(b)$ such that, for every $N$ with $1 \leq N \leq N(b)$, there exists at least one equilibrium $(y(n), q(n \mid m)$, where $q(n \mid m)$ is uniform, supported on $\left[a_i, a_{i+1}\right]$ if $m \in\left(a_i, a_{i+1}\right)$,
- $U^S\left(\bar{y}\left(a_i, a_{i+1}\right), a_i, b\right)-U^S\left(\bar{y}\left(a_{i-1}, a_i\right), a_i, b\right)=0, \quad (i=1, \ldots, N-1)$
- $y(n)=\bar{y}\left(a_i, a_{i+1}\right) \quad$ for all $n \in\left(a_i, a_{i+1}\right)$,
- $a_0=0$, and
- $a_N=1$.
Further, any equilibrium is essentially equivalent to one in this class, for some value of $N$ with $1 \leq N \leq N(b)$.
Remarks:
- 第一个说的是均衡中对sender的条件，看图第一行，图中$t_1$是$m_1$和$m_2$的分割点，那么这个情况下发$m_1$或者$m_2$对sender的收益应该是一样的，否则sender就会选择收益更高的那个，这个是indifference条件
- 第二个说的是均衡中对receiver的条件，原本的那个他会选择收益更高的那个式子是算的后验，现在和这个新定义的（算先验的最优）是等价的
The Quadratic Example
The Setting
Quadratic形容的是两个人的收益函数
- $U^R(y, m) = - (y-m)^2$
- $U^S(y, m) = - (y-(m+b))^2, \quad b>0$
- 然后$f(m)$是uniform的
The Equilibrium
给定一个信号，代表着区间$a_i, a_{i+1}$，那么这时候receiver的最优动作是
\[\bar{y}\left(a_i, a_{i+1}\right)=\left(a_i+a_{i+1}\right) / 2, \quad i=0, \ldots, N-1 .\]因为
\[\begin{aligned} &\arg \max_y \int_{\underline{a}}^{\bar{a}} U^R(y, m) f(m) d m \\ =& \arg \max_y \int_{a_i}^{a_{i+1}} -(y-m)^2 d m \\ =& \arg \max_y \frac{1}{3}[(y-a_{i+1})^3 - (y-a_i)^3] \\ =& \arg \max_y -(a_{i+1}-a_i) y^2 + (a_{i+1}^2 - a_i^2) y - \frac{1}{3}(a_{i+1}^3 - a_i^3) \\ =& -\frac{(a_{i+1}^2 - a_i^2)}{ - 2 (a_{i+1}-a_i)} \\ =& \frac{a_{i+1} + a_i}{2} \end{aligned}\]然后根据theorem 1中的receiver的限制了，现在看sender的情况，也就是一个state下分割的两个message的收益期望应该是相等的
\[-\left(\frac{a_i+a_{i+1}}{2}-a_i-b\right)^2=-\left(\frac{a_{i-1}+a_i}{2}-a_i-b\right)^2\]然后用单调性推导一下
\[\begin{aligned} -\left(\frac{a_i+a_{i+1}}{2}-a_i-b\right)^2 =& -\left(\frac{a_{i-1}+a_i}{2}-a_i-b\right)^2 \\ \left(\frac{a_{i+1}-a_i}{2}-b\right)^2 =& \left(\frac{a_{i-1}-a_i}{2}-b\right)^2 \\ \frac{a_{i+1}-a_i}{2}-b = \frac{a_i - a_{i-1}}{2}+b \quad &\text{or} \quad \frac{a_i-a_{i+1}}{2}+b = \frac{a_i - a_{i-1}}{2}+b \\ \end{aligned}\]第二种情况会推出$a_{i+1}=a_{i-1}$所以不可能，所以是第一种情况，化简为
\[a_{i+1}=2a_i-a_{i-1}+4b\]（好像不用写那么细…）
然后是求解这个递推公式的通项公式，移项发现$a_{i+1}-a_i = a_i - a_{i-1}+4b$，然后$a_0=0$，换元$b_i = a_i - a_{i-1}$很好解，得到
\[a_i = a_1 i + 2i(i-1)b\]Mixed Motives and Honesty
那么现在看一下这个区间最多能分成几份，记为$N(b)$，这个$a_i$是递增的，最后那个数不能超过上界$1$，可以看出就是求最大的$i$，$2i(i-1)b<1$，得到
\[N(b) = \mathrm{ceil}\left( -\frac{1}{2} + \frac{1}{2} \left( 1+\frac{2}{b} \right)^{1/2} \right)\]- 所以可以看出$b$越小（越靠近0），那么$N(b)$越大。这意味着他们的interests越aligned，那么可以把这个区间分得越多，也就是说信息的模糊性就会很小，意味着可以发很多信息
- 如果$b$变大，那么就是uninformative的情况，不管什么state都只能划分一个区间，只能发一个信号；在这个例子中，只要$b$超过$1/4$就只能发一个信号了
Comparison with Bayesian Persuasion
Kamenica, Emir, and Matthew Gentzkow. “Bayesian persuasion.” American Economic Review 101.6 (2011): 2590-2615. 这个例子是写在了Section 6.2 Preference Disagreement里
这里偷个懒就按bp这篇文章里的notation，不改了
- Receiver’s utility: $u=-(a-\omega)^2$
- Sender’s utility: $v=-\left(a-\left(b_1+b_2 \omega\right)\right)^2$
还是先看receiver会怎么做，他会选择一个$\hat{a}$来最优化自己的收益期望，他肯定是要让动作接近他认为的state，也就是动作等于后验下的$state$的期望$\hat{a}(\mu)=\mathbb{E}_\mu[\omega]$
那么现在有了receiver的行为，那么看sender的收益，代入$a$到收益函数里是
\[\hat{v}(\mu)=-b_1^2+2 b_1\left(1-b_2\right) E_\mu[\omega]-b_2^2 E_\mu\left[\omega^2\right]+\left(2 b_2-1\right)\left(E_\mu[\omega]\right)^2\]BP的formulation是以下（根据Corollary 1，也就是simplification）：
\[\begin{aligned} & \max _\tau E_\tau\left[-b_1^2+2 b_1\left(1-b_2\right) E_\mu[\omega]-b_2^2 E_\mu\left[\omega^2\right]+\left(2 b_2-1\right)\left(E_\mu[\omega]\right)^2\right] \\ & \text { s.t. } \int \mu d \tau(\mu)=\mu_0 . \end{aligned}\]其中一大堆东西都是常数across all Bayes-plausible $\tau$’s：$-b_1^2+2 b_1\left(1-b_2\right) E_\mu[\omega]-b_2^2 E_\mu\left[\omega^2\right]$$
- $-b_1^2$很明显是常数
- $E_\mu[\omega]$单独看不是常数，但是$E_\tau[E_\mu[\omega]] = E_\tau[E_\mu[\omega]]$
- $E_\tau[E_\mu[\omega^2]] = E_\tau[E_\mu[\omega^2]]$
这个优化问题等价于
\[\begin{array}{ll} \max _\tau E_\tau\left[\left(2 b_2-1\right)\left(E_\mu[\omega]\right)^2\right] \\ \text { s.t. } \int \mu d \tau(\mu)=\mu_0 . \end{array}\]如果$b_2$
- 大于$1/2$，这个问题就是strictly convex的，full disclosure is uniquely optimal
- 小于$1/2$，这个问题就是strictly concave的，no disclosure is uniquely optimal
- 等于$1/2$，all mechanisms yield the same value
这是因为文章里的Proposition 8，要证的
- Proposition 8: For any prior,
- if $\hat{v}(\mu)$ is (strictly) concave, no disclosure is (uniquely) optimal;
- no disclosure: $\mu = \mu_0$.
- if $\hat{v}(\mu)$ is (strictly) convex, full disclosure is (uniquely) optimal;
- full disclosure: $\mu(\cdot\mid\sigma)$ is degenerate for all $\sigma$ sent in equilibirum. $\mu$ is degenerate if there is $s$ s.t. $\mu(s) = 1$.
- if $\hat{v}(\mu)$ is convex and not concave, strong disclosure is (uniquely) optimal.
- strong disclosure: $\mu$ is at the boundary of $\Delta(s)$ for all $\sigma$ sent in equilibirum. (?)
注意到，这个问题和$b_1$根本没关系
- 也就是他们之间的interests差距再大也可以优化
- 对比cheap talk中的说法是$b_1$如果大于$1/4$就不可能通信了
- 原因解释如下（有点抽象）：The reason for this difference is that Sender’s commitment frees him from the temptation to try to increase the average level of Receiver’s action, the temptation which is so costly both for him and for Receiver in the equilibrium of the cheap talk game.
- 感觉是说有了commitment就不会无限制地greedy
Signaling
和cheap talk对应的一个概念是signaling，发信号需要cost
历史情况是，先有的signaling，认为这是比较直接的东西，然后后面才发展了cheap talk，后面认为cheap talk很广泛很重要，再后面才是persuasion
目前下面部分是从wiki里复制的，具体还没去细看
Questions
- Effort: How much time, energy, or money should the sender (agent) spend on sending the signal?
- Reliability: How can the receiver (the principal, who is usually the buyer in the transaction) trust the signal to be an honest declaration of information?
- Stability: Assuming there is a signalling equilibrium under which the sender signals honestly and the receiver trusts that information, under what circumstances will that equilibrium break down?
Job Marketing
In the job market, potential employees seek to sell their services to employers for some wage, or price. Generally, employers are willing to pay higher wages to employ better workers. While the individual may know their own level of ability, the hiring firm is not (usually) able to observe such an intangible trait—thus there is an asymmetry of information between the two parties. Education credentials can be used as a signal to the firm, indicating a certain level of ability that the individual may possess; thereby narrowing the informational gap. This is beneficial to both parties as long as the signal indicates a desirable attribute—a signal such as a criminal record may not be so desirable. Furthermore, signaling can sometimes be detrimental in the educational scenario, when heuristics of education get overvalued such as an academic degree, that is, despite having equivalent amounts of instruction, parties that own a degree get better outcomes—the sheepskin effect.